reading-notes

Trees

Source: Trees

Terms

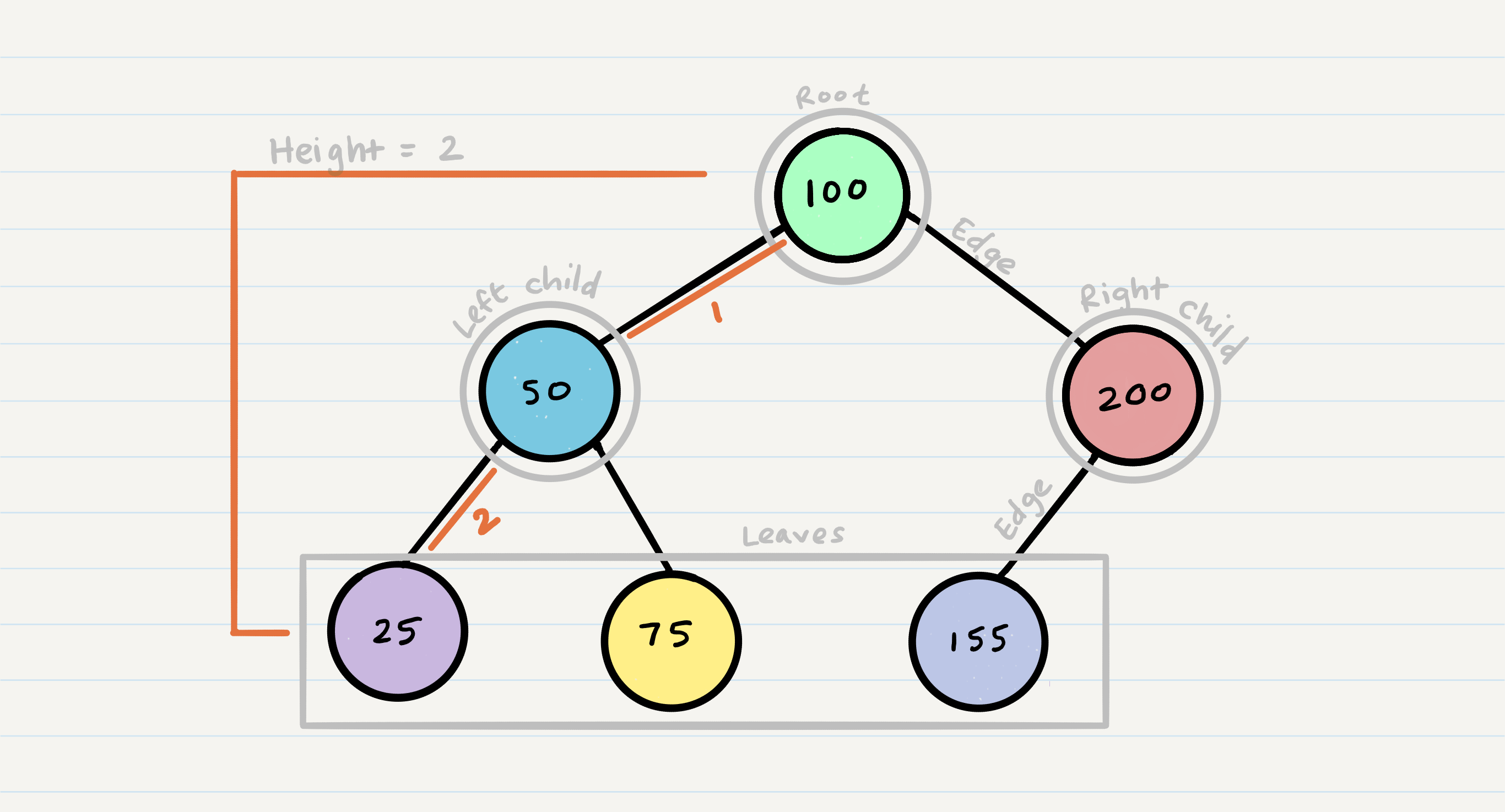
• Node - Individual item in the tree
• Root - First/top node in the tree
• Left Child - Node positioned to left of a node or root
• Right Child - Node positioned to right of a node or root
• Edge - Link between parent and child node
• Leaf - Node that contains no children
• Height - Number of edges from root to bottommost node

Traversing Depth First

Prioritze going depth (height) first.

Common to use recursion to search, using the call stack to navigate back up after the end

Types

1. Pre-order - root » left » right
   • Print root, then search down left recursively
   • Once left is null, search down right recursively
   • When a leaf is hit, we pick up the rest of the function call

   ALGORITHM preOrder(root)
    // INPUT <-- root node
    // OUTPUT <-- pre-order output of tree node's values
   
    OUTPUT <-- root.value
   
    if root.left is not Null
        preOrder(root.left)
   
    if root.right is not NULL
        preOrder(root.right)
   

2. In-order - left » root » right

   ALGORITHM inOrder(root)
    // INPUT <-- root node
    // OUTPUT <-- in-order output of tree node's values
   
    if root.left is not NULL
        inOrder(root.left)
   
    OUTPUT <-- root.value
   
    if root.right is not NULL
        inOrder(root.right)
   

3. Post-order - left » right » root

   ALGORITHM postOrder(root)
    // INPUT <-- root node
    // OUTPUT <-- post-order output of tree node's values
   
    if root.left is not NULL
        postOrder(root.left)
   
    if root.right is not NULL
        postOrder(root.right)
   
    OUTPUT <-- root.value
   

Traversing Breadth First

Prioritze going breadth (width) first.

Traditionally uses a queue, instead of call stack/recursion

1. Add root, A, to queue
2. Dequeue node A to check it
3. Enqueue left B and then right C
4. B is now in front of queue
5. Repeat!
   • Dequeue B
   • Enqueue D and E

ALGORITHM breadthFirst(root)
// INPUT  <-- root node
// OUTPUT <-- front node of queue to console

  Queue breadth <-- new Queue()
  breadth.enqueue(root)

  while breadth.peek()
    node front = breadth.dequeue()
    OUTPUT <-- front.value

    if front.left is not NULL
      breadth.enqueue(front.left)

    if front.right is not NULL
      breadth.enqueue(front.right)

Binary Trees

Trees with only two children per node.

No specific sorting order by definition

Adding - Typical to fill all child spots, but not required. This would use ‘breadth’ first traversal

Big O Time: Adding is O(n).
Big O Space: Breadth first, O(w) w=wdith

Binary Search Tree

Trees where all nodes smaller than root are on left, larger on right.

Searching: Traverse side based on comparison to n

Best approach is a while loop until you hit leaf or node you’re searching for

Big O Time: Adding is O(h), h=height
Big O Space: O(1)